Talk:Sulbasutra

By Krishna Maheshwari

The Sulbasutras are appendices to the Vedas which give rules for constructing altars with mathematical precision. Most of Vedic mathematics contained these Sulbasutras but given the purpose being a manual for altar construction, do not give proofs of how these formula were derived. Some of the rules, such as the method of constructing a square of area equal to a given rectangle, are exact, while others, such as constructing a square of area equal to that of a given circle, are based on approximations.

Little is known about the authors of the Sulbasutras other then their names and a rough indication of the period in which they lived. Like many ancient mathematicians our only knowledge of them is their writings. The most important of these documents are the Baudhayana Sulbasutra and the Apastamba Sulbasutra. Others include the Manava Sulbasutra and the Katyayana Sulbasutra. Several mathematical concepts from these sutra are given in this article.

Given that these are manuals for construction, it is fair to assume that there must have been a rich mathematical tradition that discovered and proved these rules as well as the output of the construction that is described. By way of analogy, a construction manual for a bull-dozer would not derive each of the mathematical rules required to build the components of the bull-dozer--they would be assumed and only the steps required for construction would be given. A similar approach is taken with these manuals.

Pythagoras's theorem

The Pythagoras theorem given by the Greek mathematician Pythagoras had already been provided in the Sulbasutras hundreds of years before even the birth of Pythagoras. The sulbasutras provide several specific cases as well as generic versions depending on the specific applications in altar construction.

Katyayana form of the Pythagoras Theorem

The Baudhayana Sulbasutra gives a special case of the Pythagoras theorem explicitly:

The rope which is stretched across the diagonal of a square produces an area double 
the size of the original square.

The Katyayana Sulbasutra however, gives a more general version

The rope which is stretched along the length of the diagonal of a 
rectangle produces an area which the vertical and horizontal sides make together. 

The results are stated in terms of "ropes". While thinking of explicit statements of Pythagoras's theorem, we should note that as it is used frequently there are many examples of Pythagorean triples in the Sulbasutras including (5, 12, 13), (12, 16, 20), (8, 15, 17), (15, 20, 25), (12, 35, 37), (15, 36, 39), (5/2 , 6, 13/2), and (15/2 , 10, 25/2).

Equating the area of a square to two other unequal squares

The Sulbasutras are construction manuals for yagna altars following geometric shapes and patterns such as squares, circles, rectangles, etc.

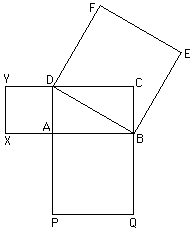
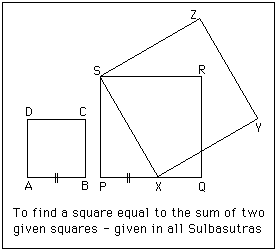
The first construction we examine occurs in many of the Sulbasutras. It is a construction for making a square equal in area to two given unequal squares.

ABCD and PQRS are the two given squares. Mark a point X on PQ so that PX is equal to AB. Then the square on SX has area equal to the sum of the areas of the squares ABCD and PQRS (SX² = PX² + PS² as per the Pythagoras Theorem).

Equating the area of a square to the area of a rectangle

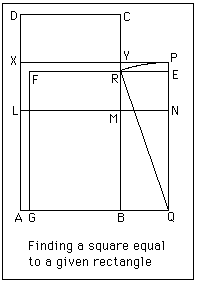
The next construction which we examine is that to find a square equal in area to a given rectangle. We give the version as it appears in the Baudhayana Sulbasutra.

The rectangle ABCD is given. Let L be marked on AD so that AL = AB. Then complete the square ABML. Now bisect LD at X and divide the rectangle LMCD into two equal rectangles with the line XY. Now move the rectangle XYCD to the position MBQN. Complete the square AQPX.

Now the square just constructed, is not the one required and a little more work is needed to complete the work. Rotate PQ about Q so that it touches BY at R. Then QP = QR and this is an ideal "rope" construction. Now draw RE parallel to YP and complete the square QEFG. This is the required square equal to the given rectangle ABCD.

As per Pythagoras's theorem

EQ2 = QR2 - RE2
       = QP2 - YP2
       = ABYX + BQNM
       = ABYX + XYCD
       = ABCD. 

Value of Pi

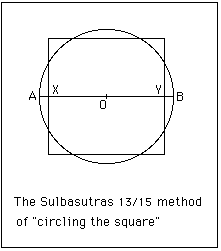
All the Sulbasutras contain a method to square the circle. It is an approximate method based on constructing a square of side 13/15 times the diameter of the given circle as in the diagram on the right. This corresponds to taking the value of n as

       n = 4 × (13/15)2 = 676/225 = 3.00444.

It is worth noting that many different values of π appear in the Sulbasutras, even several different ones in the same text. This is not surprising that whenever an approximate construction is given some value of π is implied. The authors thought in terms of approximate constructions, not in terms of exact constructions with π but only having an approximate value for it.

For example:

• Baudhayana Sulbasutra: the value of π is given as 676/225, 900/289, and 1156/361.
• In different Sulbasutras the values 2.99, 3.00, 3.004, 3.029, 3.047, 3.088, 3.1141, 3.16049 and 3.2022 can all be found.
• In the Mayana Sulbasutra: the value of π = 25/8 = 3.125

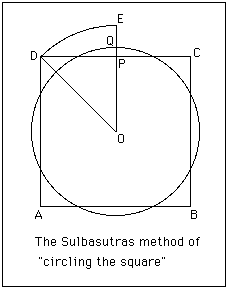
Squaring a circle

In the Apastamba sulbasutra, the authors examine the problem of squaring a circle as well as dividing a segment into seven equal parts.

The Sulbasutras also examine the converse problem of finding a circle equal in area to a given square.

The following construction appears. Given a square ABCD find the center O. Rotate OD to position OE where OE passes through the midpoint P of the side of the square DC. Let Q be the point on PE such that PQ is one third of PE. The required circle has center O and radius OQ.

Again it is worth calculating what value of π this implies to get a feel for how accurate the construction is. Now if the square has side 2a then the radius of the circle is r where

r = OE - EQ
  = √2a - 2/3(√2a - a)
  = a (√2/3 + 2/3) 

Then 4a² = πa² (√2/3 + 2/3)² which gives π = 36/(√2 + 2)² = 3.088.

Solving for the square-root of 2

Both the Apastamba Sulbasutra and the Katyayana Sulbasutra give the following approximation to √2:

Increase a unit length by its third and this third by its own fourth less the thirty-fourth part of that fourth. 

Now this gives

√2 = 1 + 1/3 + 1/(3 × 4) - 1/(3 × 4 × 34) = 577/408

which is, to nine places, 1.414215686. Compare the correct value √2 = 1.414213562 to see that the Apastamba Sulbasutra has the answer correct to five decimal places.

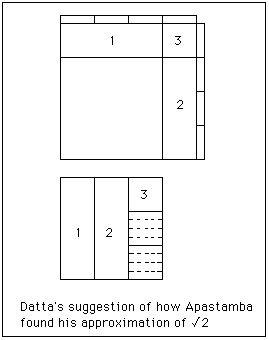
Datta considers a diagram similar to the one on the right.

The most likely reason for the construction was to build an altar twice the size of one already built. Datta's suggestion involves taking two squares and cutting up the second square and assembling it around the first square to give a square twice the size, thus having side √2. The second square is cut into three equal strips, and strips 1 and 2 placed around the first square as indicated in the diagram. The third strip has a square cut off the top and placed in position 3. We now have a new square but some of the second square remains and still has to be assembled around the first.

Cut the remaining parts (two-thirds of a strip) into eight equal strips and arrange them around the square we are constructing as in the diagram. We have now used all the parts of the second square but the new figure we have constructed is not quite a square having a small square corner missing. It is worth seeing what the side of this "not quite a square" is. It is

1 + 1/3 + 1/(3 × 4)

which, of course, is the first three terms of the approximation. Now Datta argues that to improve the "not quite a square" the Sulbasutra authors could have calculated how broad a strip one needs to cut off the left hand side and bottom to fill in the missing part which has area (1/12)². If x is the width one cuts off then

2 × x × (1 + 1/3 + 1/12) = (1/12)2

This has the solution x = 1/(3 × 4 × 34) which is approximately 0.002450980392. We now have a square who has the length of it's side as

   1 + 1/3 + 1/(3 × 4) - 1/(3 × 4 × 34)

which is exactly the approximation given by the Apastamba Sulbasutra.

Gupta gives a simpler way of obtaining the approximation for √2 than that given by Datta. He uses linear interpolation to obtain the first two terms, he then corrects the two terms so obtaining the third term, then correcting the three terms obtaining the fourth term.

Of course the method used by these mathematicians is very important to understand the depth of mathematics being produced in around the time of the authorship of the Sulbasutras.

References

• Much of this article was taken from [1] by J J O'Connor and E F Robertson